Ejemplos de ecuaciones lineales.

Factorizacion.

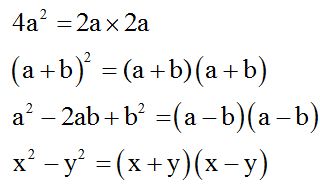
Factorización

 

 

Descomponiendo en factores el primer miembro de una ecuación de la forma x2+mx+n=0 ax2+bx+c=0 se obtiene un método muy rápido para resolver la ecuación.

 

Resolver x2+5x-24=0 por descomposición en factores. Facturando el trinomio (145), se tiene:

(X+8) (x-3)=0

Para que el producto (x+8) (x-3) sea cero es necesario que por lo menos uno de estos factores sea cero, es decir, la ecuación se satisface para x+8 y x-3=0.

 

Podemos, pues, suponer que cualquiera de los factores es cero.

Si x+8=0, se tiene que x=-8

Y si x-3=0, se tiene que x=3.

Lo anterior nos dice que x puede tener los valores -8 ó 3. Por tanto, -8 y 3 son las raíces de l ecuación dada.

R. x1= -8. X2=3.

Por tanto, para resolver una ecuación de 20 grado por descomposición en factores:

• (A)Se simplifica la ecuación y se pone en la forma x2+mx+n=0 o ax2+bx+c=0.

 

•  (B)Se factora el tinomio del primer miembro de la ecuación.

 

 

• (C)Se igualan a cero cada uno de los factores y se resuelven las ecuaciones simples que se obtiene de este modo.

 

Formula General.

 

La formula nos dice: la raíz de una ecuación de segundo grado con una incógnita es igual al coeficiente del segundo termino con le signo cambiado, mas o menos la raiz cuadrada de la diferencia entre el cuadrado de dicho coeficiente y el cuádruplo del producto del coeficiente del primer termino por el termino independiente, todo dividido por el duplo del coeficiente del primer termino.

La formula da directamente las raíces o soluciones de una ecuación de segundo grado del tipo indicado, luego se deduce que será preciso transformar las ecuaciones hasta reducirlas a este tipo para poder aplicarle la formula.

 

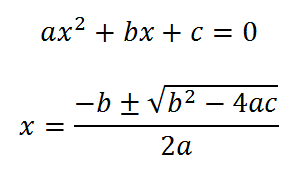
Ecuaciones de segundo grado Incompletas

Son ecuaciones de la forma ax² +c = 0 Que carecen del termino en x o de la forma ax²+bx = 0
Que carecen del termino independiente.

Ejemplo:  x^{2  _} 16 = 0 y 3x²  +5x = 0 Son ecuaciones incompletas de segundo grado.

 

Ecuaciones de Segundo Grado Completas

Son ecuaciones en la forma  x²+bx+c =0, que  tiene un término en x², un término en x y un término independiente de x . 

Así, 2x²+7x-15=0 y x²-8x= -15 ó x²- 8x+15=0 son ecuaciones completas de segundo grado.

METODO DE COMPLETAR EL CUADRADO PARA RESOLVER LA ECUACION DE SEGUNDO GRADO.

Para comprender mejor este metodo,consideremos primero la ecuacion del tipo :
x²+bx+c = 0
Podemos escribir esta ecuacion del siguiente modo:
x²+bx = -c
Si observamos el primer miembro veremos que el binomio x²+bx le falta un termino para hacer un trinomio cuadrado perfecto.
Tal termino es el cuadrado de la mitad del coeficiente del segundo termino
(b/2)²  o lo que es lo mismo b²/4.
En efecto,formamos asi un trinomio cuyo primer termino es el cuadrado de x; su segundo termino es el doble producto de x por (b/2) ; y su tercer termino es el cuadrado de la miad del coeficiente del segundo termino (b/2)²  o sea   b²/4. Para que no se altere la ecuacion le agregamos al segundo miembro la misma cantidad que le agregamos al primer miembro.
Asi tendremos: x²+bx+( b²/4.) = ( b²/4.) - c
En el primer miembro de esta ecuacion tenemos un trinomio cuadrado perfecto.
Factorizamos: (x+b/2)² =  b²/4 - c
Extraemos la raiz cuadrada a ambos miembros.
Cuando el coeficiente de x² = es mayor que 1,el procedimiento es esencialmente el mismo,solo que como el primer paso dividimos los tres terminos de la ecuacion entre a,
coeficiente de  x²  .

Fuente: Algebra Baldor.

 

ECUACIÓN DE SEGUNDO GRADO

Es toda ecuación en la cual, una vez simplificada, el mayor exponente de la incógnita es 2.
Ejemplo: 4x+7x+6=0.

Las ecuaciones de segundo grado,se dividen en :




Fuente: Algebra Baldor.

Tipos de ecuaciones cuadráticas (segundo grado).